Parallel And Perpendicular Lines Quizlet
Parallel and Perpendicular Lines
How to utilise Algebra to find parallel and perpendicular lines.
Parallel Lines
How practice we know when two lines are parallel?
Their slopes are the same!
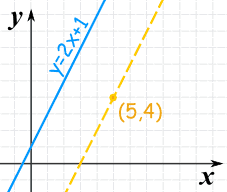
Example:
Observe the equation of the line that is:
- parallel to y = 2x + 1
- and passes though the indicate (5,4)
The slope of y=2x+i is: 2
The parallel line needs to take the same gradient of ii.
We can solve it using the "point-slope" equation of a line:
y − y1 = ii(10 − x1)
And and so put in the point (5,4):
y − 4 = 2(ten − 5)
And that answer is OK, but allow's likewise put information technology in y = mx + b form:
y − 4 = 2x − 10
y = 2x − 6
Vertical Lines
But this does not work for vertical lines ... I explain why at the terminate.
Not The Same Line
Be careful! They may be the same line (only with a unlike equation), and so are not parallel.
How exercise nosotros know if they are really the same line? Check their y-intercepts (where they cross the y-centrality) every bit well as their slope:
Example: is y = 3x + ii parallel to y − 2 = 3x ?
For y = 3x + 2: the slope is 3, and y-intercept is two
For y − 2 = 3x: the gradient is three, and y-intercept is 2
In fact they are the same line and and then are non parallel
Perpendicular Lines
Two lines are Perpendicular when they meet at a right angle (ninety°).
To find a perpendicular gradient:
When one line has a slope of one thousand, a perpendicular line has a gradient of −ane m
In other words the negative reciprocal
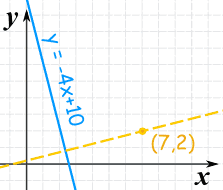
Example:
Detect the equation of the line that is
- perpendicular to y = −4x + 10
- and passes though the signal (7,two)
The slope of y=−4x+ten is: −4
The negative reciprocal of that slope is:
m = −i −4 = 1 4
So the perpendicular line will accept a slope of 1/iv:
y − yone = (1/four)(x − xi)
And now put in the point (7,2):
y − 2 = (ane/4)(ten − seven)
And that answer is OK, but let'south also put information technology in "y=mx+b" form:
y − 2 = ten/4 − 7/4
y = x/4 + one/4
Quick Check of Perpendicular
When nosotros multiply a slope m by its perpendicular slope −ane m we get merely −1.
So to quickly check if two lines are perpendicular:
When we multiply their slopes, we go −1
Like this:
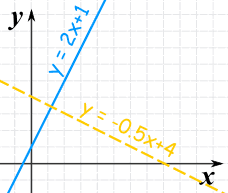
Are these ii lines perpendicular?
| Line | Slope |
| y = 2x + 1 | two |
| y = −0.5x + 4 | −0.v |
When nosotros multiply the two slopes we get:
2 × (−0.v) = −one
Yes, we got −i, so they are perpendicular.
Vertical Lines
The previous methods work nicely except for a vertical line:
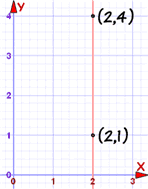
In this case the gradient is undefined (as we cannot divide by 0):
m = yA − yB xA − xB = 4 − i 2 − 2 = 3 0 = undefined
And then just rely on the fact that:
- a vertical line is parallel to some other vertical line.
- a vertical line is perpendicular to a horizontal line (and vice versa).
Summary
- parallel lines: same gradient
- perpendicular lines: negative reciprocal slope (−1/m)
Parallel And Perpendicular Lines Quizlet,
Source: https://www.mathsisfun.com/algebra/line-parallel-perpendicular.html
Posted by: combstuncland.blogspot.com


0 Response to "Parallel And Perpendicular Lines Quizlet"
Post a Comment